Welcome to DSA Visualizer

Our goal is to deliver clear understanding and visualization of the Data Structures and Algorithms knowledge.

Array

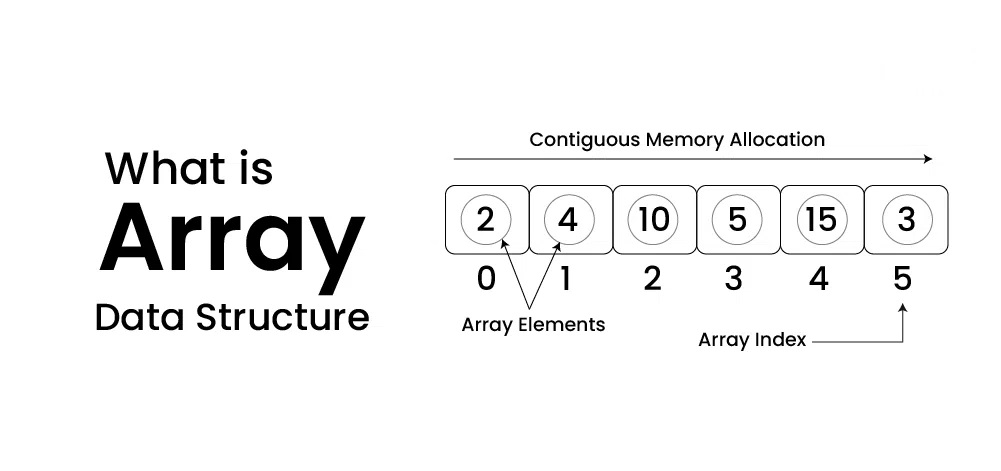
An array is a fundamental data structure in computer science that stores a collection of elements in contiguous memory locations. This arrangement enables efficient access through indexing, allowing elements to be retrieved in constant time. Arrays are widely used for organizing and manipulating data due to their simplicity and speed, making them ideal for tasks like sorting and searching. However, their fixed size can limit flexibility compared to other data structures. Overall, arrays are essential for implementing various algorithms and applications in programming.

What is Array

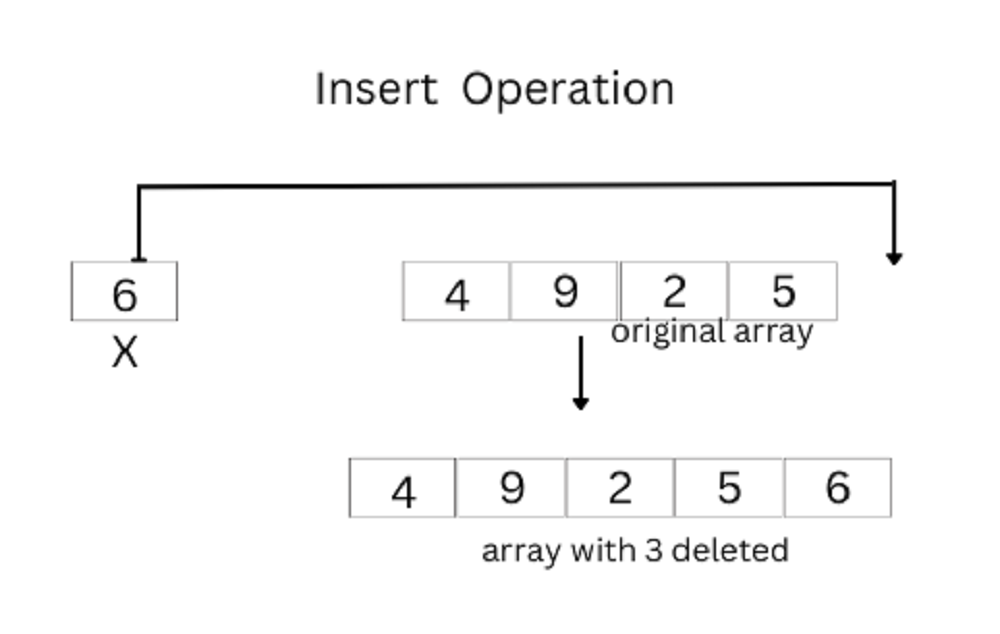
Insert Operation

1. Insert at the end: In an unsorted array, the insert operation is faster as compared to a sorted array because we don’t have to care about the position at which the element is to be placed.

2. Insert at any position:Insert operation in an array at any position can be performed by shifting elements to the right, which are on the right side of the required position.

Insert Operation

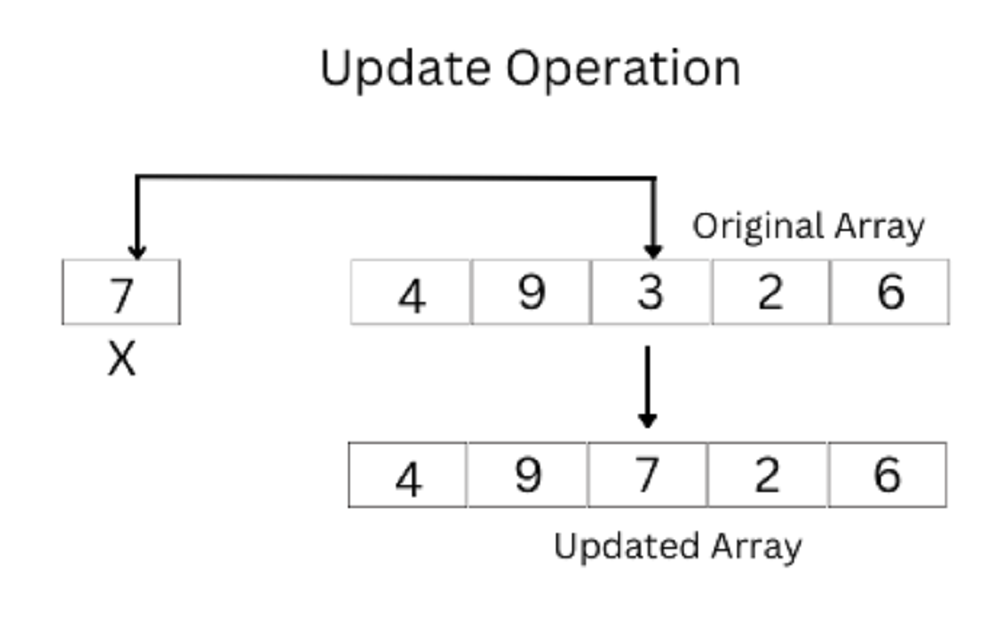
Update Operation

Updating an element in an array means changing the value of a specific element at a given index. This operation is generally straightforward and involves the following steps:

1. Access the Element: To update an element, you first need to access it using its index. In an array, this is done in constant time O(1).

2. Modify the Value: After accessing the element, you can assign a new value to it. This operation also takes constant time O(1).

Insert at Position

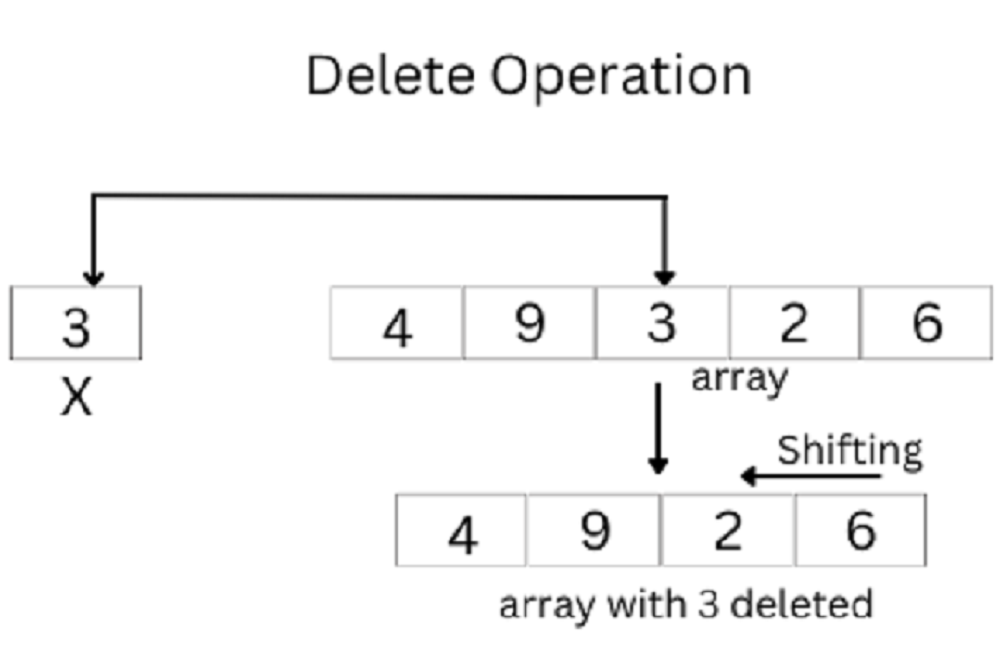
Delete Operation

In the delete operation for an array, the process begins by searching for the target element using linear search, which involves iterating through the array to locate the element's index. Once found, the deletion is performed by shifting all subsequent elements one position to the left, effectively overwriting the deleted element. This ensures that there are no gaps in the array. After shifting, it’s important to update the array's size to reflect the removal. Optionally, the last element can be set to a default value to avoid confusion. This method maintains the integrity of the array while allowing for efficient element removal.

Delete Operation

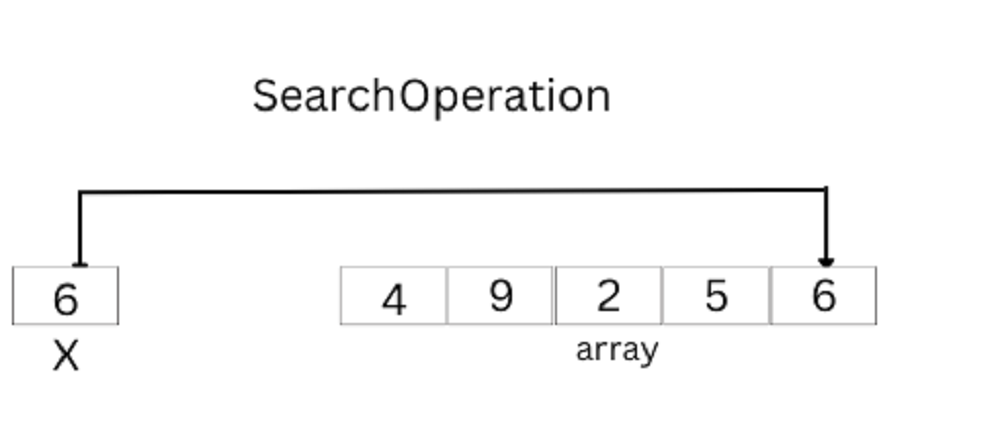
Search Operation

In an unsorted array, the search operation is typically performed using linear traversal. This involves iterating through the array from the first element to the last. During the traversal, each element is compared to the target value being searched for. If a match is found, the index of the element is returned, indicating its position in the array. If the traversal completes without finding the target, a message indicating that the element is not present can be returned. This approach is straightforward and effective, though it has a time complexity of O(n), making it less efficient for large datasets compared to more advanced search methods.

Search Operation

Linked List

A linked list is a data structure used in computer science to organize a sequence of elements. Each element, or "node," contains two parts: the data itself and a reference (or "link") to the next node in the sequence. This allows for efficient insertion and deletion of elements, as nodes can be easily rearranged without shifting the entire list. Unlike arrays, linked lists don't require contiguous memory locations, making them more flexible for certain operations. However, accessing elements in a linked list can be slower compared to arrays, as it typically requires traversing the list from the beginning to reach a specific node.

Node Diagram

Insert

Inserting a new element into a linked list involves adding a node to the list while maintaining the list's structure. There are different types of insertion operations depending on where you want to add the new node:

  • Insert At Head

    Node Diagram
    • Objective: Add a new node at the start of the linked list.
    • Process:
    • Create a new node.
    • Set the new node's next pointer to point to the current head of the list.
    • Update the head of the list to point to the new node.

  • Insert At Tail

    • Objective: Add a new node at the end of the linked list.
    • Process:
    • Traverse the list to find the last node.
    • Create a new node.
    • Set the last node's next pointer to the new node.
    • Set the new node's next pointer to null.
    Node Diagram

  • Insert At Any Position

    Node Diagram
    • Objective: Add a new node at a specific position in the linked list.
    • Process:
    • Traverse the list to find the node at the position before the desired insert position.
    • Create a new node.
    • Set the new node's next pointer to the next pointer of the previous node.
    • Update the previous node's next pointer to the new node.

Delete

Deleting a node in a linked list involves updating the pointer of the preceding node to bypass the node being removed. If the node to delete is the head, the head pointer is updated to the next node, and the memory of the removed node is freed. This ensures the list remains properly linked and functional.

  • Delete At Head

    Node Diagram
    • Objective: Remove the first node from the linked list.
    • Process:
    • Identify the current head of the linked list.
    • Set the head pointer to point to the next node in the list, effectively removing the current head node from the list.
    • Free the memory allocated for the old head node to avoid memory leaks.
    • Update the linked list’s head reference to the new first node.
    • Ensure all references to the old head node are removed or updated appropriately.

  • Delete At Tail

    • Objective: Remove the last node from the linked list.
    • Process:
    • Traverse the list to find the second-to-last node.
    • Set the second-to-last node's next pointer to null.
    • Free the memory of the last node.
    Node Diagram

  • Delete At Any Position

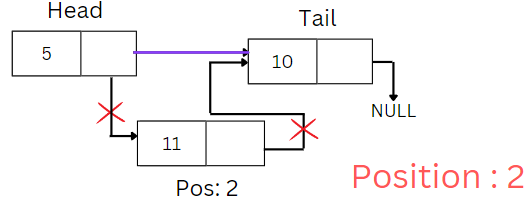
    Node Diagram
    • Objective: Remove a node at a specific position in the linked list.
    • Process:
    • Traverse the list to find the node just before the desired position.
    • Update the previous node's next pointer to skip the node to be deleted.
    • Free the memory of the node to be deleted.

Update

Updating a node in a linked list involves traversing the list to locate the node at a specific index or with a given value. Once identified, the node's value is modified to the new value. If the node is not found, an appropriate error or indication is given.

  • Update By Value

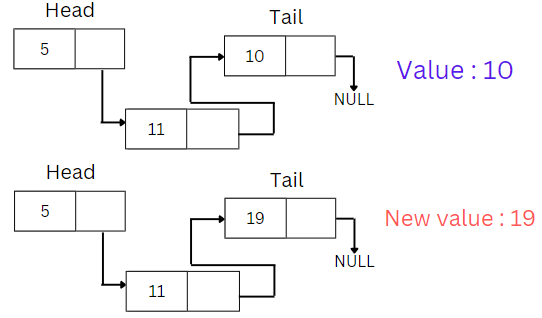
    Node Diagram
    • Objective: Update the value of a node in the linked list based on its value.
    • Process:
    • Traverse the list to find the node with the target value.
    • Update the node's value with the new value.

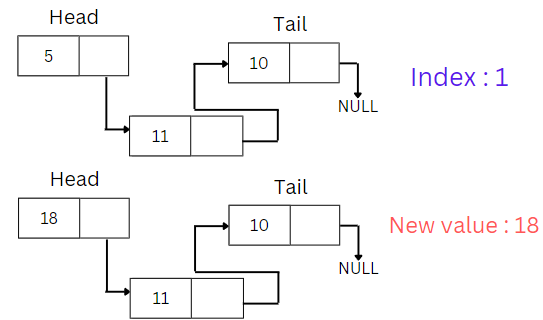
  • Update By index

    • Objective: Update the value of a node at a specific index in the linked list.
    • Process:
    • Traverse the list to the node at the specified index.
    • Update the node's value with the new value.
    Node Diagram

Search

Searching in a linked list involves traversing the list from the head to find a node with a specific value or at a given index. If the node is found, its value or position is returned; otherwise, an indication of the absence is provided.

  • Search By Value

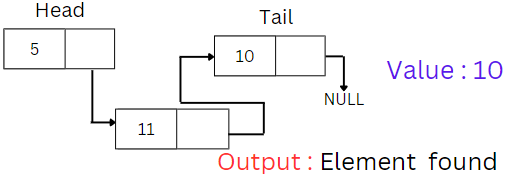
    Node Diagram
    • Objective: Find a node with a specific value in the linked list.
    • Process:
    • Traverse the list while comparing each node's value to the target value.
    • If the value is found, return the node or its position.
    • If the end of the list is reached without finding the value, indicate that the value is not present.

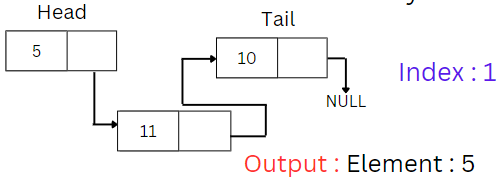
  • Search By index

    • Objective: Retrieve the value of the node at a specific index in the linked list.
    • Process:
    • Traverse the list to the node at the specified index.
    • Return the node's value.
    • If the index is out of bounds, indicate an error or that the index is invalid.
    Node Diagram

Stack

A stack is a linear data structure that follows the Last In, First Out (LIFO) principle, meaning that the last element added to the stack is the first one to be removed. It can be visualized as a collection of items stacked on top of each other, similar to a stack of plates. The primary operations of a stack are push, which adds an element to the top of the stack, and pop, which removes the top element. Stacks are widely used in programming and computer science for various applications, including function call management in recursion, undo mechanisms in applications, and parsing expressions. Due to their structure, stacks can efficiently handle specific problems where order of processing is crucial. However, they also have limitations, such as the risk of stack overflow if too many elements are pushed onto the stack beyond its capacity.

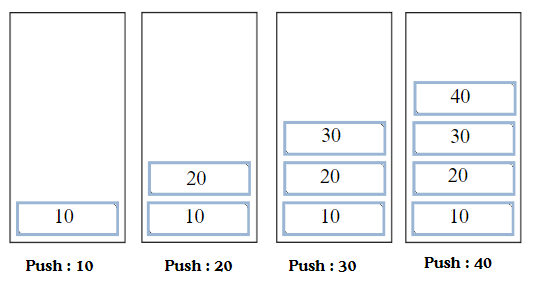
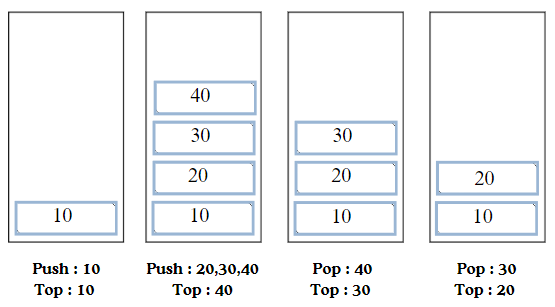
Push Operation

    Push Operation in stack is used to insert elements to stack

    Stack Overflow : Special condition when element is pushed and stack is full

    Example: Assume size of stack is 5

  • Push 10 to Stack
  • Push 20 to Stack
  • Push 30 to Stack
  • Push 40 to Stack
  • Push 50 to Stack
  • Push operation fails
    Stack Overflow !! Stack size is 5
Push Operation

Pop Operation

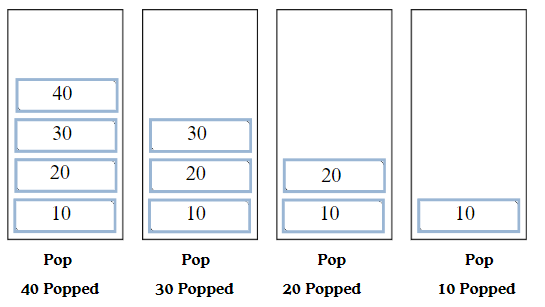
Pop Operation

    Pop operation is used to remove elements from stack

    Stack Underflow : Special condition when stack is empty and still element is popped

    Example: Assume size of stack is 4

  • Pop 40 from stack
  • Pop 30 from stack
  • Pop 20 from stack
  • Pop 10 from stack
  • Pop operation fails
    Stack Underflow !! Stack is Empty

Display Top Element

    In this operation, the top element of the stack is displayed

    LIFO : As stack is Last In First Out, therefore element inserted at last is removed first

  • Case : 1
    Top : 10
  • Case : 2
    Top : 40
  • Case : 3
    Top : 30
  • Case : 4
    Top : 20
  • Display operation fails
    Stack is Empty !! No top element
Display Top Element

Queue

A queue is a linear data structure that follows the First In, First Out (FIFO) principle, meaning that the first element added is the first to be removed. It is similar to a real-life queue, where people line up, and the person at the front is served first. Queues are commonly used in situations where order is important, such as scheduling processes in operating systems, managing tasks in printers, or handling requests in web servers. Basic operations include enqueue (inserting an element at the rear), dequeue (removing an element from the front), peek (viewing the front element), and checking if the queue is empty or full. Queues can be implemented using arrays, linked lists, or other dynamic structures, and they play a crucial role in various algorithms and applications across computer science.

Enqueue Operation

Enqueue Operation
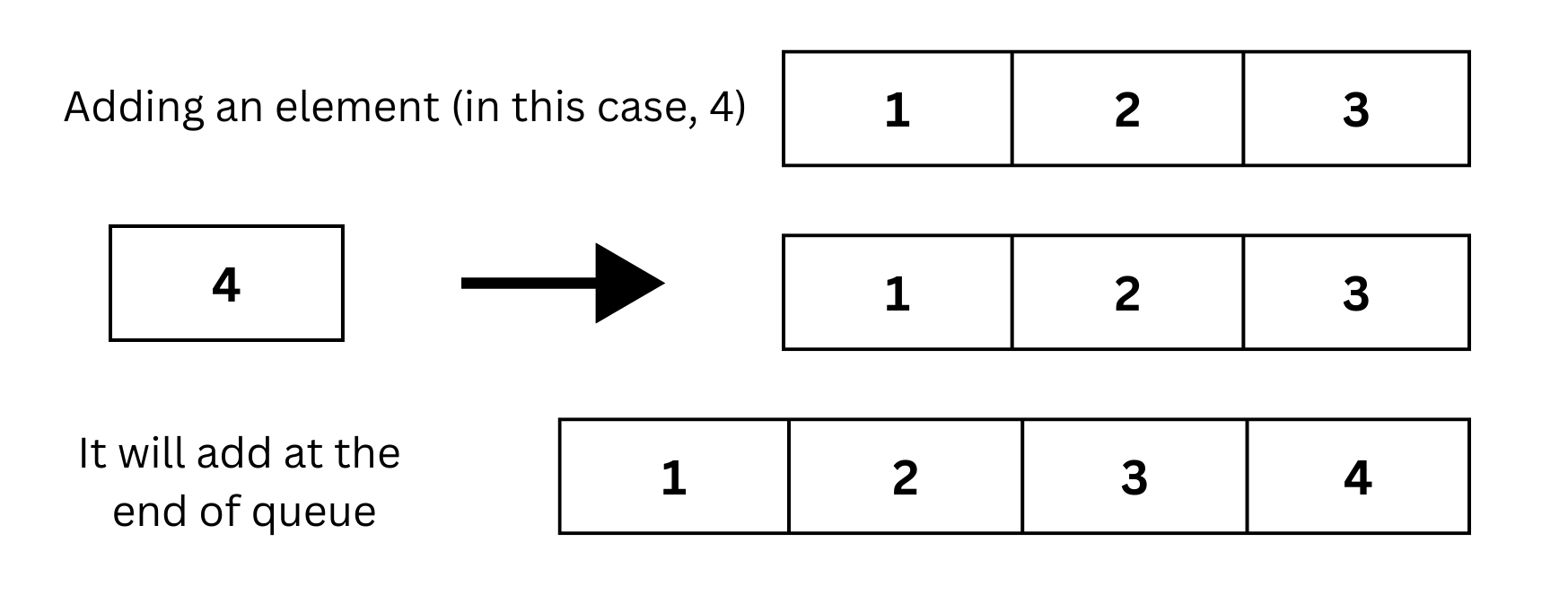
  • The enqueue operation adds an element to the end (rear) of the queue.
  • It follows the First-In-First-Out (FIFO) principle.
  • After enqueuing, the new element is placed after the last element in the queue.
  • Example: Queue [1, 2, 3], enqueue 4 → [1, 2, 3, 4]

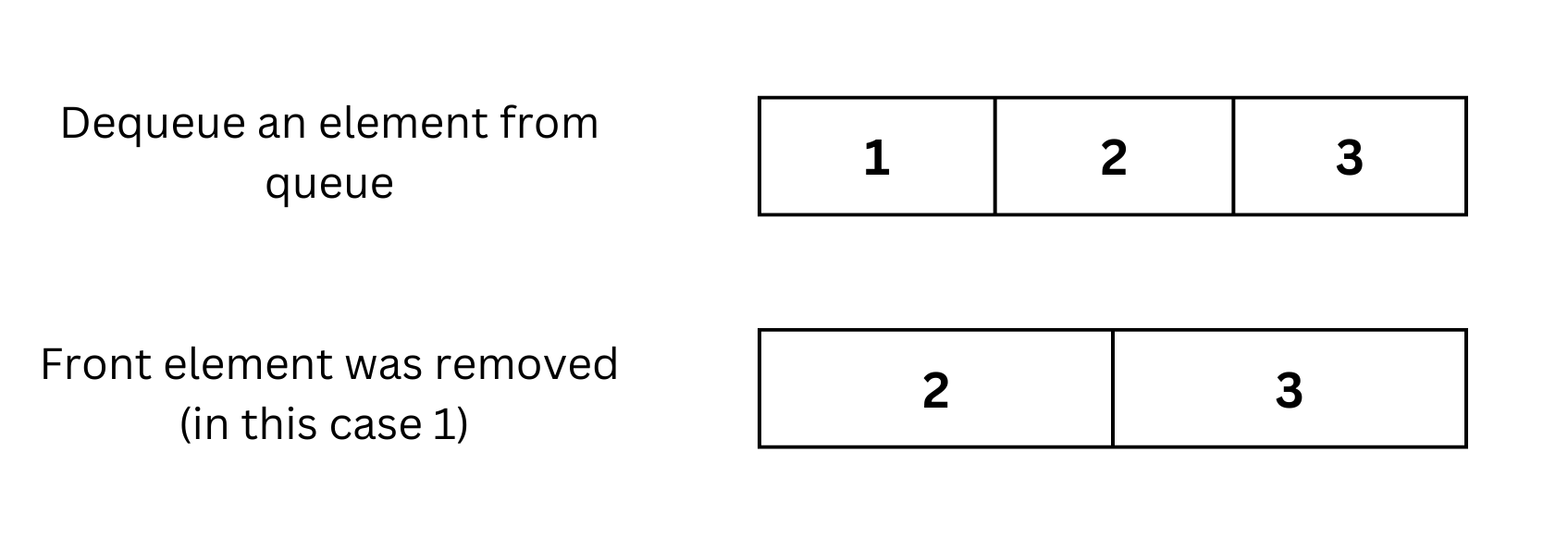
Dequeue Operation

  • The dequeue operation removes an element from the front of the queue.
  • The oldest element in the queue is removed first, adhering to the FIFO principle.
  • Once dequeued, the queue shrinks by removing the first element.
  • Example: Queue [1, 2, 3], dequeue → [2, 3]
Dequeue Operation

Front Element

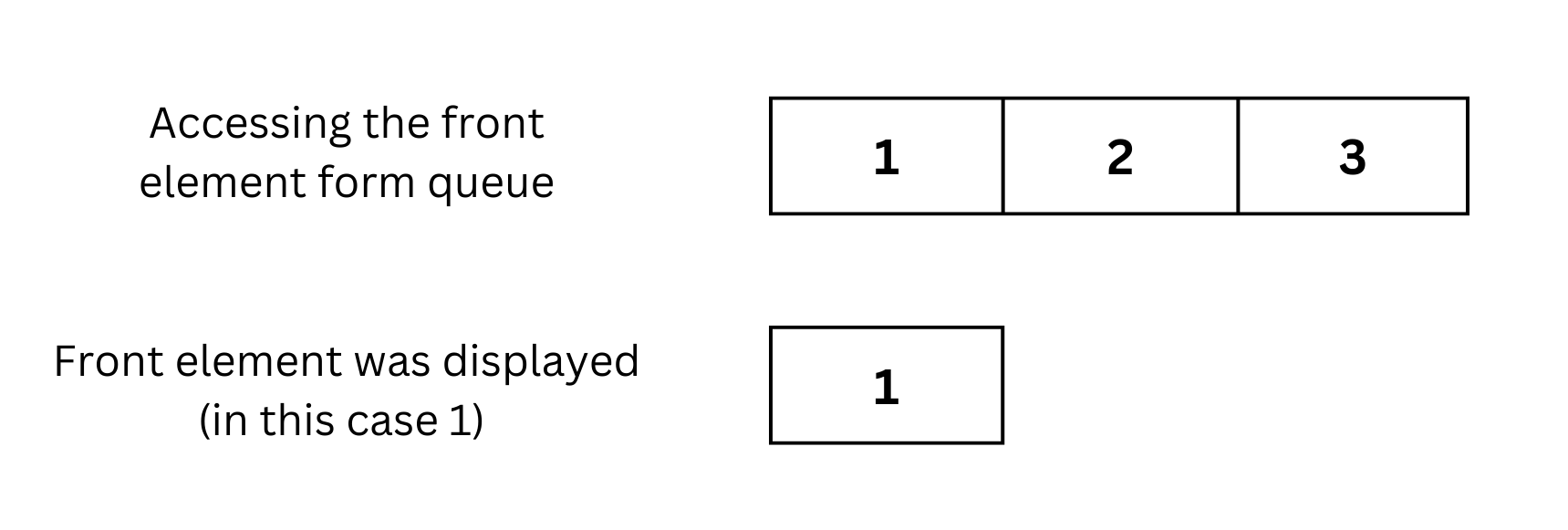
Front Operation
  • The front operation retrieves the element at the front without removing it.
  • This helps in checking which element is next in line to be dequeued.
  • It is useful when you need to inspect the next item without modifying the queue.
  • Example: Queue [1, 2, 3], front → 1